Work
Energy
The Concept of Energy
Explain the concept of energy
Energy can be defined as capacity of doing work.
Energy has the same SI unit like that of work, and that is Joules (J)
S.I Unit of Energy
State S.I unit of energy
Energy has the same SI unit like that of work, and that is Joules (J)
Different Forms of Energy
Identify different forms of energy
There are different forms of energy such as:
- Chemical energy
- Heat energy
- Light energy
- Sound energy
- Electrical energy
- Nuclear energy
- Solar energy
Difference between Potential Energy and Kinetic Energy
Distinguish between potential energy and kinetic energy
There are two types of chemical energy, which are:
- Potential energy:It is the energy possessed by a body mass in its position or state.
- Kinetic energy: It is the energy possessed by a body due to its motion.
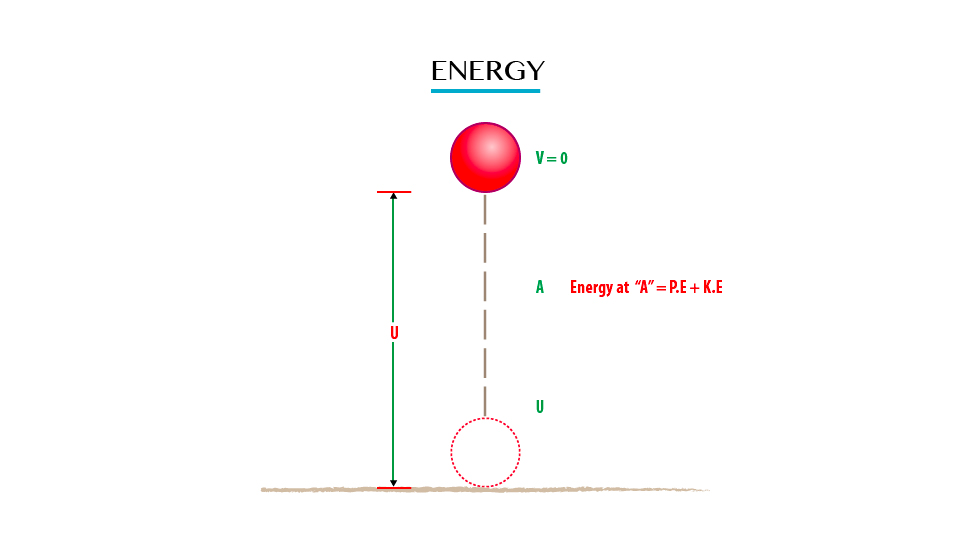
Consider when the body is vertically thrown upwards with an initial velocity ‘u’ from the ground.
At the ground:The height is zero and initial velocity is at maximum so as to attain maximum height.
Therefore K.E = ½ MV2 will be maximum
K.Emax = ½ mv2
Where K.E = Kinetic energy
M = Mass of the object/body
V=Velvety
P.E = Mgh
Where
P.E = Potential energy
M= Mass of the object
H = Height of the object
g = gravitation force
P.E = Mgh will be zero because P.E
= M*g*0 (body at the ground where k=0)
Neglecting
the air resistance, as the body moves upwards its velocity decreases it
also experiences gravitational force (g) pulling downwards towards the
earth’s centre.
the air resistance, as the body moves upwards its velocity decreases it
also experiences gravitational force (g) pulling downwards towards the
earth’s centre.
The maximum Height Attained
The final velocity of the body will be zero (V=0)
Therefore K.E = ½ mv2
K.E = ½ m(0)2
K.E = 0
P.E = MgHmax
Note:That
the object drops from Hmax that is; it leaves with zero Kinetic Energy.
At position A in fig. 8. The conservation of mechanical energy (M.E) is
given as:
the object drops from Hmax that is; it leaves with zero Kinetic Energy.
At position A in fig. 8. The conservation of mechanical energy (M.E) is
given as:
P.E + K.E = Constant
(The sum of P.E and K.E is constant throughout the motion of the object if the air resistance is neglected)
The Transformation of Energy
Explain the transformation of energy
The notion of energy is that energy is changed from one form into different forms using transducers.
Transducer is a device used to transform energy from one form to another.
For example:
- Battery converts chemical energy into electrical energy.
- A generator converts mechanical energy into electrical energy.
- A motor converts electrical energy into mechanical energy.
The Table Summarising Energy Transformation
| ORIGINAL ENERGY | TRANSDUCER | ENERGY TRANSFORMED |
| Chemical energy | Battery | Electrical energy |
| Chemical energy | Motor | Chemical energy |
| Mechanical energy | Generator | Electrical energy |
| Solar energy | Solar panel | Electrical energy |
| Chemical energy | Motor car | Mechanical energy |
| Electrical energy | Microphone | Sound energy |
| Electrical energy | Heater | Heat energy |
Activity 1
To demonstrate pressure of potential energy.
Materials and Apparatus
- A heavy stone
- A bucket full of water
- A strong inelastic rope; and
- Smooth pulley
Procedures:
- Collect the heavy stone, using a strong rope tie it to a bucket of water
- Pass the rope over smooth pulley fixed to a support.
- Hold stationary the heavy stone at height “h” above the ground
- Release the stone
Results and observations:
- When the stone released the bucket of water will start to rise.
- The stone is said to have potentials energy because of its position above the ground.
- Lifting a body of mass “m” to a height “h” above the ground requires work to be done against gravity. Work = Mgh
Example 2
A ball of mass 0.5 kg is kicked vertically upwards and rises to a height of 5m. Find the potential energy by the ball.
Data given:
Mass of the ball (Mb) = 0.5 kg
Height (h) = 5m
Gravitation force (g) 10N/kg
Potential energy (P.E) = ?
Solution:
Potential energy (P.E)= mgh
= 0.5kg x 10N/kg x 5m
= 25 NM
1NM= 1Joules
Potential energy (P.E) = 25 Joules.
Activity 2
Aim: to investigate the law of conservation of energy by a simple pendulum.
Materials and Apparatus:A pendulum bob and light inelastic string.
Producers
- Pull the bob of a simple pendulum in position A so that it is at height “h” above position B.
- Release the bob so that it swings to position C via the lowest position B and back to A.
- Consider the figure below:
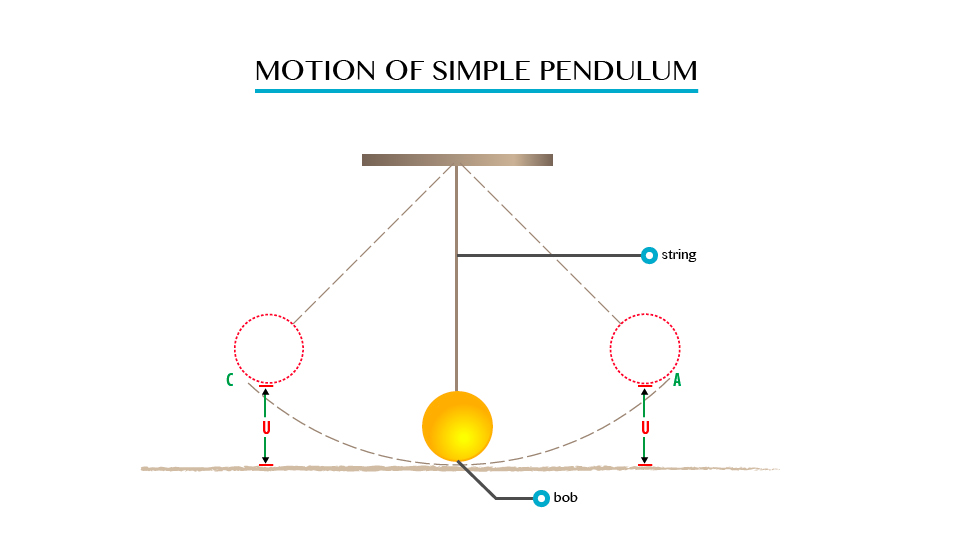
Observation
When the bob is at position A, it possesses potential energy only due to the height “h” which is equal to “Mgh”.
As it swings downwards to position B, the height decreases, and as the result it loses potential energy.
- The bob has Vmax and hence K.Emax at B. The height at B is zero, thus the P.E is zero.
- As
it swings towards C, the P.E increases and reaches its maximum again in
position C, where the Kinetic Energy is zero. At position D, the energy
of the bob is party potential and party Kinetic.
The Principle of Conservation of Energy
State the principle of conservation of Energy
The
law of conservation of energy state that “ Energy can neither be
created nor destroyed but can only be converted from one form to
another.”
law of conservation of energy state that “ Energy can neither be
created nor destroyed but can only be converted from one form to
another.”
This means the amount of energy is constant all the time.
Example 3
A
stone of mass 2kg is released form a height of 2m above the ground.
Find the potential energy of the stone when it is at the height of 0.5m
above the ground.
stone of mass 2kg is released form a height of 2m above the ground.
Find the potential energy of the stone when it is at the height of 0.5m
above the ground.
Data given;
Mass of the stone (Ms) = 2kg
Height released (h) = 2m
Gravity (g) = 10N/kg
Potential energy = (P.E) ?
Solution:
P.E at height g 2m
P.E = Mgh
= 21g x 10N/kg x 2m
P.E = 40 Joules
P.E at 2m = 40Joules
Than P.E at height of 0.5m
= 21g x 10N/kg x 0.5m
P.E at 0.5m = 10Joules
100s of P.E = 40 Joules – 10Joules
= 30 Joules
According
to conservation of energy the loss of P.E should be equal to the gain
in K.E, when the air resistance is neglected.
to conservation of energy the loss of P.E should be equal to the gain
in K.E, when the air resistance is neglected.
K.E of the stone at 0.5 above the ground = 30 Joules
Example 4
A
ball of mass 0.21kg is dropped from a height of 20m. on impact with the
ground it loses 30J of energy. Calculate the height which it reaches on
the rebound.
ball of mass 0.21kg is dropped from a height of 20m. on impact with the
ground it loses 30J of energy. Calculate the height which it reaches on
the rebound.
Data given;
Mass of ball (Mb) = 0.2kg
Height dropped (h) = 20m
Loose in energy (E) 30J
Height which reaches=?
Solution;
Consider the figure below;
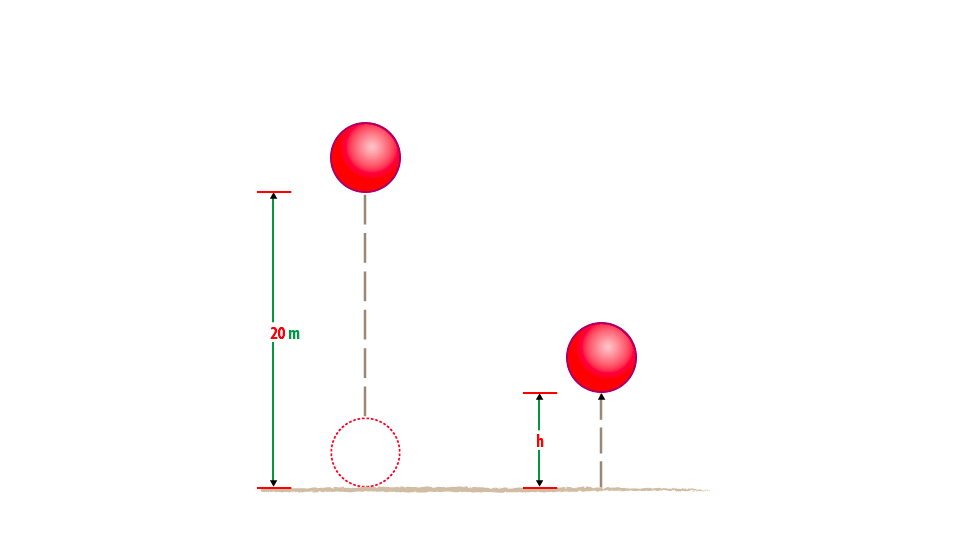
At 20m above ground the initial energy of the ball = Mgh
= 0.2kg x 10N/kg x 20m
= 40 Joules.
So after the impact the ball loose 30J and the energy remaining is 40 J-10J
= 10Joules
At the top of rebound the energy of the ball = potential energy (P.E)
The height reaches (h) is 5m.
Uses of Mechanical Energy
Explain the uses of mechanical energy
The
mechanical energy can be used to produce electric power using
generators. Some uses of mechanical energy are: It enables our body to
do work, it makes work easier and faster, it is used to transport goods
and people from one place to another, many transport vehicles uses the
knowledge of mechanical energy. Examples of vehicles which uses
mechanical energy are aeroplanes and motor cars.
mechanical energy can be used to produce electric power using
generators. Some uses of mechanical energy are: It enables our body to
do work, it makes work easier and faster, it is used to transport goods
and people from one place to another, many transport vehicles uses the
knowledge of mechanical energy. Examples of vehicles which uses
mechanical energy are aeroplanes and motor cars.
Power
The Concept of Power
Explain the concept of power
Power is the rate of which work is done.
- It is a measure of the rate at which energy changes.
- This means that whenever work is done energy changes into a different form.
The S.I Unit of Power
State the S.I unit of power
The SI unit of power is Jules per second J/S or watts, W.
1 Joules per second = 1 watt
When 1 Joules of work is done per second the power produced is a watt. Watt is the unit for measuring electrical power.
The Rate of Doing Work
Determine the rate of doing work
Suppose
that two cranes each lift objects having masses of 200kg to a height of
12m. Crane A lifts its object in 10sec while crane B requires 15sec to
lift its object. Assume they lift the objects at a constant velocity
they do the same amount of work.
that two cranes each lift objects having masses of 200kg to a height of
12m. Crane A lifts its object in 10sec while crane B requires 15sec to
lift its object. Assume they lift the objects at a constant velocity
they do the same amount of work.
Work done = GPE
= Mgh
= (200kg) (9.8m/s2)(12m)
= 23520J
Each did a work that was equivalent to 23520J.
What is different for the two cranes is the rate at which they did the work or their generation of power.
The power of crane A can be calculated by;
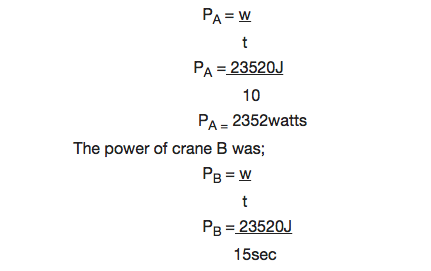
PB = 1568 watts.
Example 5
How much power is required to accelerate a 1000kg car from rest to 26.7m/s in 8sec?
Solution:
The work done on the car increases its Kinetic energy.
Work done = AKE
½ MV2 – ½ MV2
The power required is given by:
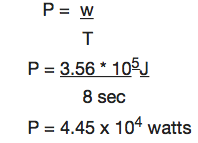
Example 6
Car engine is rated in horsepower (hp) where 1hp = 746watts. What is the required power measured in horsepower?
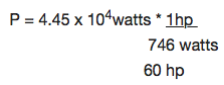
Since work causes a change in energy. DE power can be considered as the rate of change of energy.
P = DE/t
Hi, i think that i saw you visited my blog thus i
came to “return the favor”.I am trying to find things to improve my web site!I suppose its
ok to use some of your ideas!!
Hello I am so happy I found your web site, I really found you by
mistake, while I was researching on Yahoo for something else, Anyhow
I am here now and would just like to say thank you for a
remarkable post and a all round exciting blog (I also love the
theme/design), I don’t have time to read through it all at the minute but I have book-marked
it and also included your RSS feeds, so when I have time I will be
back to read much more, Please do keep up the awesome work.
Hello are using WordPress for your site platform?
I’m new to the blog world but I’m trying to get started and create my
own. Do you need any coding knowledge to make your own blog?
Any help would be greatly appreciated!