State the importance of measurement in real life
Measurements are so often taken for granted, we sometimes do not appreciate the grand importance measurements play in our lives. On a baseline level, measurements fall into the categories of weight, area, volume, length and even temperature. While we look at these various categories as stoic forms of mathematical measurements, a closer examination of things we do in everyday life reveals their clear importance.
Taking proper medicine. If you are ill (whether a serious or minor illness) you need to take your medicine and take it in the proper amount. If you take too little or too much then you are not going to get the proper benefit from it.
Keeping yourself warm or cool. If the temperature outside dips or increases you have to make an adjustment on your thermostat in order to remain at a safe and healthy temperature. Understanding the measurement scale of a thermostat is critical in this regard or else you may find yourself feeling rather uncomfortable.
Understanding weight. Is that object too heavy to pick up by yourself or do you need to use something to lift it? Some may think this is not important but it is pretty easy to hurt yourself if you lift objects that are too heavy.
Structure. This was saved for last because it is the common theme that is found in all the multitude of reasons for the importance of measurements. Measurements provide structure and remove the chaos that would result without any congruent method of understanding weight, mass, temperature, etc.
| Basic physical quantity | SI unit |
| Mass | Kilogram (kg) |
| Length | Meter (m) |
| Time | Second(s |
Metric system
More than 1 unit
Giga(G) = 1,000,000,000 (10ˆ9)
- Mega(M) = 1,000,000 (10ˆ6)
- Kilo(K) = 1,000(10ˆ3)
- Hector (h) = 100(10ˆ2)
- Decca(da) = 10(10ˆ1)1
- Deci (d) = 1/10 (10ˆ-1)
- Cent (c) = 1/100(10ˆ-2)
- Mill (m) = 1/1000 (10ˆ-3)
- Micro(μ) = 1/1,000,000(10ˆ-6)
- Vernier caliper
- Micrometer screw gauge
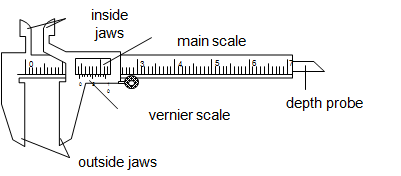
The main scale is graduated in centimeter (cm) while the vernier scale is graduated in millimeter (mm).The vernier scale is a short scale 9mm long divided into 10 equal parts, so that the difference in length between a vernier division and the main scale division is 0.1mm or 0.01cm.
The main scale reading is recorded. This is the reading which precedes the zero mark of the vernier scale.
The vernier scale reading is recorded by reading the mark on it which coincide with a mark on the main scale (i.e. vernier scale reading x 0.01cm).
The summation of these two readings is the length of the object measured.
A micrometer screw gauge:Is an instrument used to measure length to the accuracy of 0.001cm(0.01mm).It is used to measure the diameters of wires and ball bearings. It can measure small lengths up to about 2.5cm.The diagram below describes the micrometer screw gauge.
It consists of a spindle which is fitted with a graduated thimble. The screwed portion of a spindle is totally enclosed to protect it from damage.The pitch of the screw is 0.5mm, so that the spindle moves through o.o5cm for each complete turn.
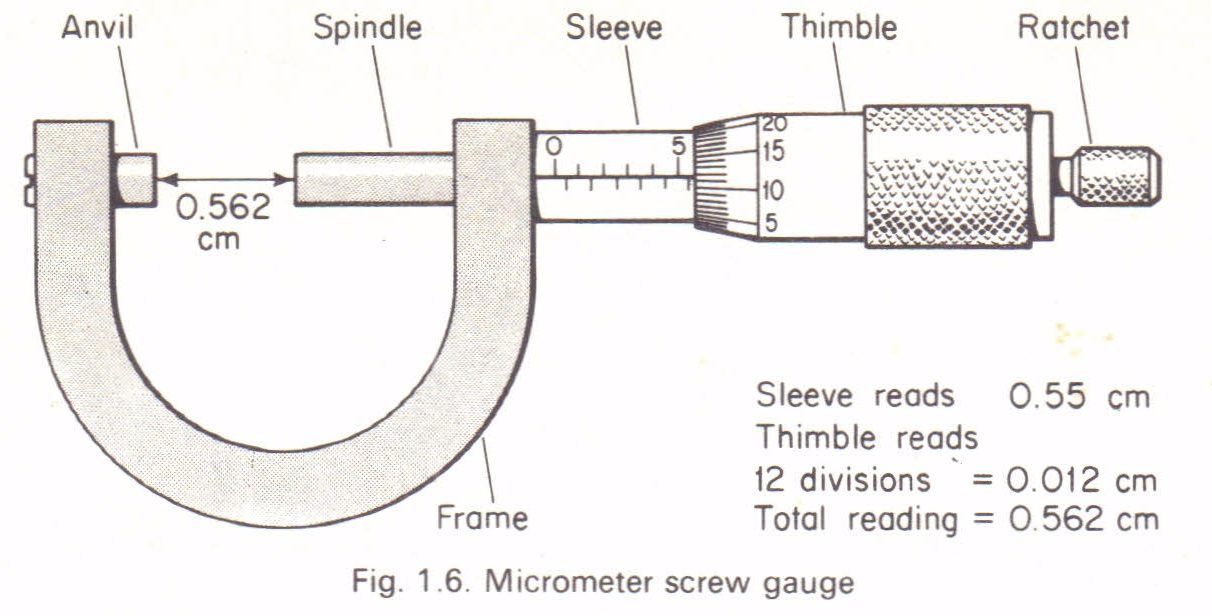
Sleeve reading is recorded. This gives the units and the first two decimal places in mm.
Thimble reading is then recorded. This gives the third decimal place (thimble reading x 0.001mm).
The summation of these two readings gives the diameter of the object under measurement.
Before use,the faces of anvil and spindle should be wiped clean to remove any dirty particle which would give false readings.
Check and record for zero error then + or –the correction to the final answer.
Mass
The mass of a body doesn’t change from place to place. The instrument used to measure mass is called a beam balance.
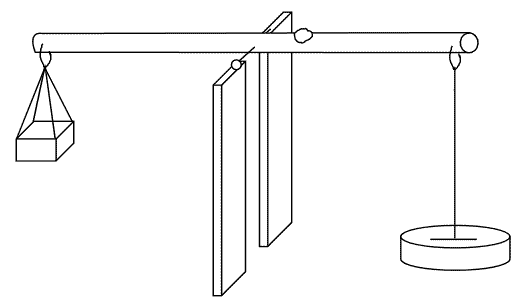
| Mass | Weight |
| Is the amount of matter contained | Is the force by which the earth pull a body to its centre |
| SI unit is kilogram | SI unit is Newton |
| Doesn’t vary from place to place on the earth’s surface | Varies from place to place on the earth’s surface |
| Measured by beam balance | Measured by a spring balance |
Time
The instruments for measuring time are clocks and watches.
Derived quantities
Explain derived quantities
Derived quantities are units which are derived from the fundamental quantities. Examples are volume, density, power, work, energy, weight, frequency etc.
The S.I Units of Derived Quantities
State the S.I. units of derived quantities
SI units of Derived quantities
| Volume | Cubic meter (mˆ3) |
| Density | Kg/mˆ3 |
| Power | Watts (W) |
| Work | Joules (J) |
| Energy | Joules (J) |
| Weight | Newton (N) |
| Frequency | Hertz (Hz) |
Volume
Measuring cylinder-used for measuring or pouring out various liquids.
How to read volume measuring instruments(precautions).
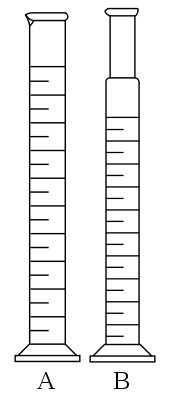
Activity 1
Materials and apparatus: Irregular object eg; stone, thread, measuring cylinder, eureka can and water.
Poor a known volume of water in a burette(V1)
Tie a stone with a thread.
Immerse the tied stone in water holding the thread and record the volume (V2)
Make sure the stone is totally immersed in water.
Volume before introducing solid = V1
Volume after introducing solid = V2
Volume of irregular solid(V3) = V2 – V1
Poor water into eureka can up to its spout
Immerse a well tied stone in water completely
Collect the overflowed water in the water.
Use a measuring cylinder to determine the volume of water collected
When a stone was introduced in an overflow can, water overflowed to the measuring cylinder.
The volume of water collected is equal to the volume of irregular object(stone)
Identify sources of errors in measurement
- Systematic errors
- Random errors
Zero error: Zero Error is caused if the reading shown is Not zero when the true value is actually zero. This is most probably caused by a flaw in the instrument for example when using a ruler that has lost its zero scale due to wear and tear hence causing an error in the measurement of length.
Wrong assumptions: For example if you assume that water boils at 100 degree Celsius but actually its boiling point is higher if there are impurities in it. (Pure water boils at 100 degree Celsius).
Lag of reaction time: For example in a sports day, when measuring a 100 m running time using a stopwatch. The observer may not press the stop button exactly when the foot of the runner touches the finishing line.
Calibration errors: Instruments that are not properly calibrated could also cause error and this has to be put in consideration when writing a report or when there is an anomaly in reading.
Taking several readings and then find the average.
Avoiding parallax error by positioning the instrument (meter rule) properly on the table with the eyes perpendicular to the scale.
Some instruments can be adjusted to eliminate zero error. For example when using an ammeter, there is an adjuster to set the indicator to zero before making any measurement.
In the case of a ruler, measurement can be carried out starting from the next clear scale for example if scale 0.0cm is blurred, we can start measuring the length from 2.0cm, of course taking the difference of value in consideration when recording the final reading.
The mass of the rectangular block is m.
The volume of the rectangular block will be calculated by multiplying the obtained length, l height, h and width, w.
Volume, V = l x h x w, But; Density = mass/volume
The volume of a material can be obtained by using various methods depending on the shape of the material
Obtain the mass of the given object using the beam balance.
Fill water to the measuring cylinder to the volume V₁.
Immerse the well tied irregular object totally in the cylinder containing water.
Record the new volume V₂.
- Volume of irregular object = V₂ – V₁
- Mass obtained = M
Record the mass of the empty beaker m₁ using a beam balance.
Pour the known volume of kerosene into the beaker by using bur rete, V.
Record the mass of the beaker and kerosene m₂.
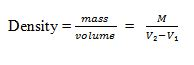
Definition of the Relative Density of a Substance
Define the relative density of a substance
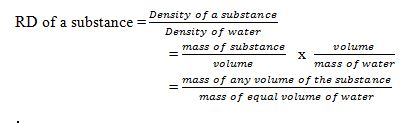
Applications of Density and Relative Density in Real Life
Interpret applications of density and relative density in real life
It is the key factor which is considered during the design of various structures and equipment. Eg. ships and planes.
Density is considered during the selection of materials.
Density is also considered during the design of equipment used in swimming.