GEOMETRIC AND TRANSFORMATIONS
Reflection
The Characteristics of Reflection in a Plane
Describe the characteristics of reflection in a plane
A transformation in a plane is a mapping which moves an object from one position to another within the plane. Think of a book being taken from one comer of a table to another comer. Figures on a plane of paper can also be shifted to a new position by a transformation. The new postion after a transformation is called the image. Examples of transformations are reflection, rotation, enlargement and translation.
Different Reflections by Drawings
Represent different reflections by drawings
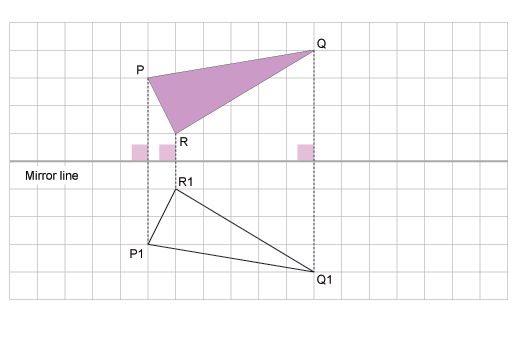
A reflection is a transformation which reflects all points of a plane in a line called the mirror-line. The image in a mirror is as far behind the mirror as the object is in front of the mirror
Characteristics of Reflection
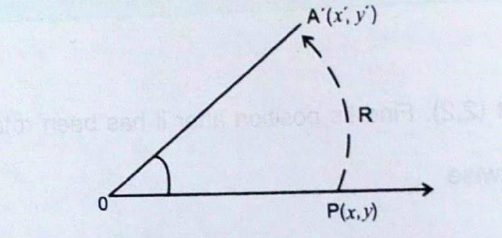
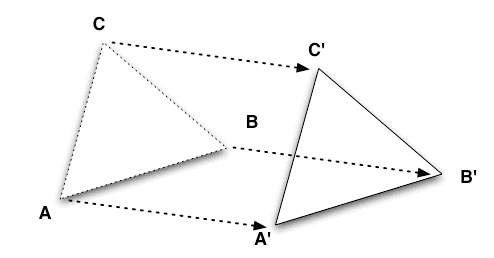
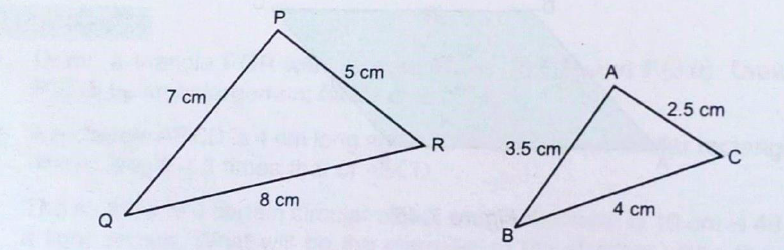
In the diagram, APQR is mapped onto ΔP’Q’R’ under a reflection in the line AB. If the paper is folded along the line AB, ΔPQR will fall in exactly onto ΔPQR. The line AB is the mirror-line. which is the perpendicular bisector of PP’, QQ’ and ΔPQR and ΔP’Q’R are congruent.
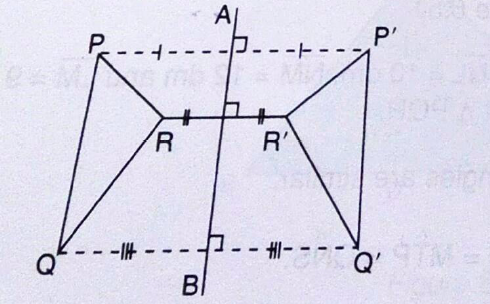
Some characteristics observed under reflection are:
- PP’ is perpendicular to AB, RR’ is perpendicular to AB and QQ is perpendicular to AB.
- The image of any point on the Q’ mirror line is the point itself.
- PP’ is parallel to RR’ and QQ’
Reflection in the Line y = x
The
line y = x makes an angle 45° with the x and y axes. It is the line of
symmetry for the angle YOX formed by the two axes. By using the
isosceles triangle properties, reflection of the point (1, 0) in the
line y = x will be (0, 1).
line y = x makes an angle 45° with the x and y axes. It is the line of
symmetry for the angle YOX formed by the two axes. By using the
isosceles triangle properties, reflection of the point (1, 0) in the
line y = x will be (0, 1).
The
reflection of (0,2) in the liney = x will be (2,0). You notice that the
co-ordinates are exchanging positions. Generally, the reflection of the
point (a,b) in the line y = x is (b,a).
reflection of (0,2) in the liney = x will be (2,0). You notice that the
co-ordinates are exchanging positions. Generally, the reflection of the
point (a,b) in the line y = x is (b,a).
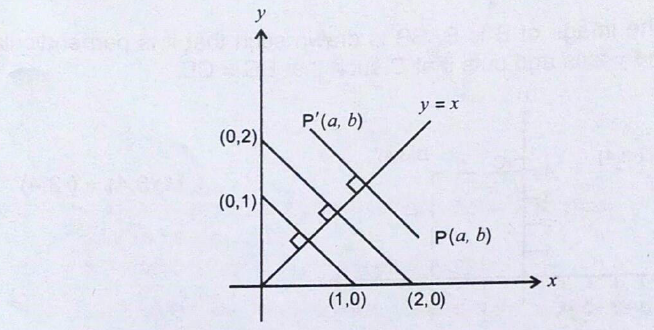
The reflection of the point B(c,d) in the line y = -x is B’ (-d, -c)
Exercise 1
- Find the image of the point D(4,2) under a reflection in the x-axis.
- Find the image of the point P(-2,5) under a reflection in the x-axis.
- Point Q(-4,3) is reflected in the y-axis. Find the coordinates of its image.
- Point R(6,-5) is reflected in the y-axis. Find the co-ordinates of its image.
- Reflect the point (1 ,2) in the line y = -x.
- Reflect the point (5,3) in the line y = x.
- Find the image of the point (1 ,2) after a reflection in the line y=x followed by another reflection in the line y = -x.
- Find
the image of the point P(-2,1) in the line y = -x followed by another
reflection in the line x = 0 ketch the positions of the image P and the
point P, indicating clearly the lines involved. - Find the co-ordinates of the image of the point A(5,2) under a reflection in the line y = 0.
- Find the coordinates of the image of the point under a reflection in the line x = 0.
- The co-ordinates of the image of a point R reflected in the x axis is R(2, -9). Find the coordinates of R.
Combined Transformations
Draw combined transformations
Combined
Transformation means that two or more transformations will be Performed
on one object. For instance you could perform a reflection and then a
translation on the same point
Transformation means that two or more transformations will be Performed
on one object. For instance you could perform a reflection and then a
translation on the same point
Example 3
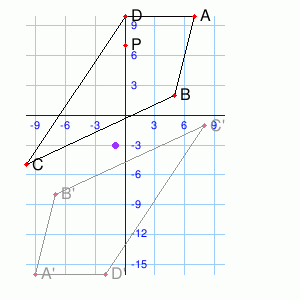
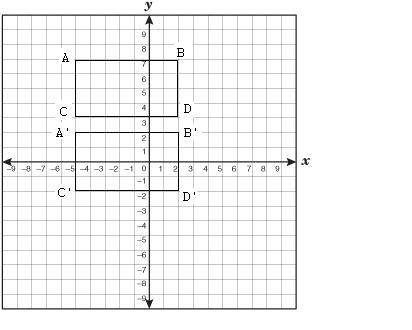
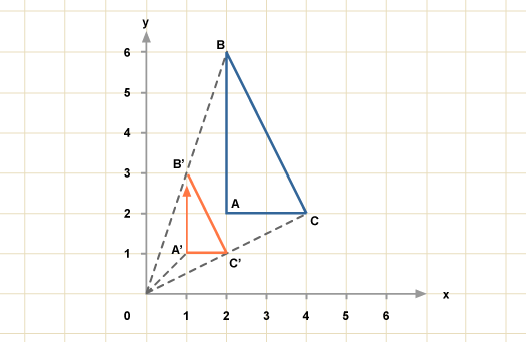
What type of transform takes ABCD to A’B’C’D’?
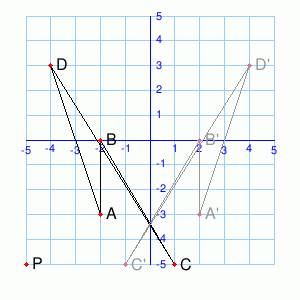
Solution
The type of transform takes ABCD to A’B’C’D’ is Reflection
Simple Problems on Combined Transformations
Solve simple problems on combined transformations
Exercise 5
What type of transform takes ABCD to A’B’C’D’?
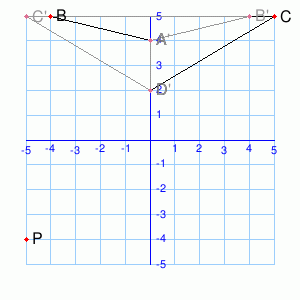
The
transformation ABCD → A’B’C’D’ is a rotation around(-1, 2)by___°.Rotate
P around(-1, 2)by the same angle. (You may need to sketch things out on
paper.)P’ = (__,__)
transformation ABCD → A’B’C’D’ is a rotation around(-1, 2)by___°.Rotate
P around(-1, 2)by the same angle. (You may need to sketch things out on
paper.)P’ = (__,__)
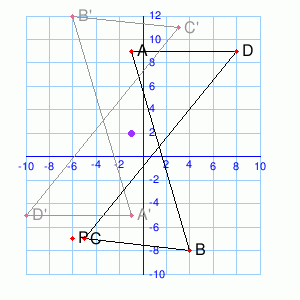
The
transformation ABCD → A’B’C’D’ is a rotation around(-1, -3)by__°Rotate P
around(-1, -3)by the same angle. (You may need to sketch things out on
paper.)P’ = (__,__)
transformation ABCD → A’B’C’D’ is a rotation around(-1, -3)by__°Rotate P
around(-1, -3)by the same angle. (You may need to sketch things out on
paper.)P’ = (__,__)