NUMBERS
We know that when we count we start 1,2 …. . But there are other numbers
like 0, negative numbers and decimals. All these types of numbers are
categorized in different groups like counting numbers, integers,real
numbers, whole numbers and rational and irrational numbers according to
their properties. all this have been covered in this chapter
categorized in different groups like counting numbers, integers,real
numbers, whole numbers and rational and irrational numbers according to
their properties. all this have been covered in this chapter
Natural and Whole Number
Natural
numbers are counting numbers. Counting always starts with 1 and
continues with 2, 3 … (dots means numbers continue with no end).
Therefore Natural or counting numbers starts from 1 and continue to
infinite (no end).
numbers are counting numbers. Counting always starts with 1 and
continues with 2, 3 … (dots means numbers continue with no end).
Therefore Natural or counting numbers starts from 1 and continue to
infinite (no end).
Natural numbers are denoted by N. natural numbers can be represented on a horizontal line called number line as shown above:
The other group of numbers starts from zero and it is called whole numbers denoted by W.
We can represent whole numbers on a number line as shown above:
The Difference between Natural and Whole Numbers
Distinguish between natural and whole numbers
Natural
numbers are either used to count one to one objects or represent the
position of an object in a sequence. They start from one and go on to
infinity.This is why they are sometimes referred to as counting numbers.
The only whole number that cannot be classified as a natural number is
0. Counting numbers can further be classified into perfect numbers,
composite numbers, co-prime/ relatively prime numbers, prime numbers,
even and odd numbers.
numbers are either used to count one to one objects or represent the
position of an object in a sequence. They start from one and go on to
infinity.This is why they are sometimes referred to as counting numbers.
The only whole number that cannot be classified as a natural number is
0. Counting numbers can further be classified into perfect numbers,
composite numbers, co-prime/ relatively prime numbers, prime numbers,
even and odd numbers.
Even ,Odd, and Prime Numbers
Identify even ,odd, and prime numbers
Even numbers are
those numbers which are divisible by 2. In other words we can say that
any natural number which can be divided by 2 is an even number. For
example 2, 4, 6, 8, 10, 12, … are even numbers since they are divisible
by 2.
those numbers which are divisible by 2. In other words we can say that
any natural number which can be divided by 2 is an even number. For
example 2, 4, 6, 8, 10, 12, … are even numbers since they are divisible
by 2.
Odd numbers are
those numbers which are not divisible by 2. In other words we can say
that any natural number when divided by 2 and remains 1 including 1 are
called odd numbers. Example 1, 3, 5, 7, 9, 11, 13, 15, … are called odd
numbers.
those numbers which are not divisible by 2. In other words we can say
that any natural number when divided by 2 and remains 1 including 1 are
called odd numbers. Example 1, 3, 5, 7, 9, 11, 13, 15, … are called odd
numbers.
Prime numbers are
those numbers which are divisible by one and itself excluding one or
any natural number which is divisible by one and itself except one. For
example 2, 3, 5, 7, 11, 13, 17, … are called prime numbers.
those numbers which are divisible by one and itself excluding one or
any natural number which is divisible by one and itself except one. For
example 2, 3, 5, 7, 11, 13, 17, … are called prime numbers.
Odd and Prime Numbers on Numbers Lines
Show even , odd and prime numbers on number lines
Odd and Prime Numbers
Operations with Whole Numbers
We have four operations which are: addition (+), subtraction (-), multiplication ( X) and division (÷).
Addition of Whole Numbers
Add whole numbers
When
adding numbers we add the corresponding digits in their corresponding
place values and we start adding from the right side i.e. from the place
value of ones to the next.
adding numbers we add the corresponding digits in their corresponding
place values and we start adding from the right side i.e. from the place
value of ones to the next.
We can add numbers horizontally or vertically.
Horizontal addition
Example 5
- 972 + 18=
- 23 750 + 250 =
Solution
- 972 + 18 = 990
- 23 750 + 250 = 24 000
Vertical addition
Example 6
Subtraction of Whole Numbers
Subtract whole numbers
Subtraction is denoted by the sign (-). It is sometimes called minus.
Subtraction is the opposite of addition. Subtraction also means reduce a
number from certain number and the answer that is obtained is called difference..
Subtraction is the opposite of addition. Subtraction also means reduce a
number from certain number and the answer that is obtained is called difference..
Subtraction
is done in similar way like addition. We subtract the corresponding
digits in their corresponding place value. For example; 505 – 13. We
first subtract ones, which are 5 and 3. Subtract3 from 5 gives 2.
Followed by tens which are 0 and 1. Subtract 1 from 0 is not possible.
In order to make it easy, take 1 from 5 (hundreds). When 1 is added to 0
it has to be changed to be tens since it is added to a place of tens.
So, when 1 comes into a place of tens it becomes 10. So add 10 to 0. We
get 10. Now, subtract 1 from 10. We get 9. We are left with 4 in a place
of hundreds since we took 1. There for our answer will be 492.
is done in similar way like addition. We subtract the corresponding
digits in their corresponding place value. For example; 505 – 13. We
first subtract ones, which are 5 and 3. Subtract3 from 5 gives 2.
Followed by tens which are 0 and 1. Subtract 1 from 0 is not possible.
In order to make it easy, take 1 from 5 (hundreds). When 1 is added to 0
it has to be changed to be tens since it is added to a place of tens.
So, when 1 comes into a place of tens it becomes 10. So add 10 to 0. We
get 10. Now, subtract 1 from 10. We get 9. We are left with 4 in a place
of hundreds since we took 1. There for our answer will be 492.
Note that similar manner will be used when subtracting.
Example 7
Multiplication of Whole Numbers
Multiply whole numbers
Multiplication
means adding repeatedly depending on the times number given. For
example; 25 6 means add 25, repeat adding 6 times i.e. 25 + 25 + 25 +
25 +25 + 25 = 150. The answer obtained after multiplying two or more
numbers is called product. The number being multiplied is called a multiplicand while the number used in multiplying is called a multiplier. Referring our example, 25 is multiplicand and 6 is multiplier.
means adding repeatedly depending on the times number given. For
example; 25 6 means add 25, repeat adding 6 times i.e. 25 + 25 + 25 +
25 +25 + 25 = 150. The answer obtained after multiplying two or more
numbers is called product. The number being multiplied is called a multiplicand while the number used in multiplying is called a multiplier. Referring our example, 25 is multiplicand and 6 is multiplier.
Example 8
Division of Whole Numbers
Divide whole numbers
Division is the same as subtraction. You subtractdivisor(the number used to divide another number) fromdividend(the
number which is to be divided), we repeat subtracting divisor to the
answer obtained until we get zero. The answer is how many times you
repeat subtraction.
number which is to be divided), we repeat subtracting divisor to the
answer obtained until we get zero. The answer is how many times you
repeat subtraction.
For
example; 27 ÷9, we take 27 we subtract 9, we get 18. Again we take 18
we subtract 9, we get 9. We take 9 we subtract 9 we get 0. We repeat
subtraction three times. Therefore the answer is 3. The answer obtained
is calledquotient. Referring to our example; 27 is
dividend, 9 is divisor and 3 is quotient. If a number can’t be divided
exactly, what remains or left over is calledremainder.
example; 27 ÷9, we take 27 we subtract 9, we get 18. Again we take 18
we subtract 9, we get 9. We take 9 we subtract 9 we get 0. We repeat
subtraction three times. Therefore the answer is 3. The answer obtained
is calledquotient. Referring to our example; 27 is
dividend, 9 is divisor and 3 is quotient. If a number can’t be divided
exactly, what remains or left over is calledremainder.
Example 9
The Four Operations in Solving Word Problems
Use the four operations in solving word problems
Sometimes
you may be given a question with mixed operations +, -, xand ÷ . We do
multiplication and division first then addition and subtraction.
you may be given a question with mixed operations +, -, xand ÷ . We do
multiplication and division first then addition and subtraction.
Example 10
- 12 ÷ 4 + 3 x 5
- 14 x2 ÷ 7 – 3 + 6
Solution
- 12 x 4 + 3 x 5 =3 + 15 (do division and multiplication fist) =18
- 14 x 2 ÷ 7 – 3 + 6 =28 ÷ 7 – 3 + 6 (multiply first) =4 – 3 + 6 (then divide) =10 – 3 (add then subtract) =7
We
may use brackets to separate x,÷ , + and – if they are mixed in the
same problem and use what is called BODMAS . BODMAS is the short form of
the following:
may use brackets to separate x,÷ , + and – if they are mixed in the
same problem and use what is called BODMAS . BODMAS is the short form of
the following:
B for Brackets O for Open D for Division M for Multiplication A for Addition and S for Subtraction
Therefore,
with mixed operations, we first do the operation inside the brackets;
we say that we open the brackets. Then we do division followed by
multiplication, addition and lastly subtraction.
with mixed operations, we first do the operation inside the brackets;
we say that we open the brackets. Then we do division followed by
multiplication, addition and lastly subtraction.
Example 11
Word problems on whole numbers
Example 12
In a school library there are 6 shelves each with 30 books. How many books are there?
Solution
Each shelf has 30 books
6 shelves have 30 × 6 = 180 books.
Therefore, there are 180 books.
Example 13
Juma’s
mother has a garden with Tomatoes, Cabbages and Water Lemons. There are
4 rows of Tomato each with 30 in it. 6 rows of Cabbages with 25 in each
and 3 rows of Water Lemo
mother has a garden with Tomatoes, Cabbages and Water Lemons. There are
4 rows of Tomato each with 30 in it. 6 rows of Cabbages with 25 in each
and 3 rows of Water Lemo
Solution
There are 30 Tomatoes in each row
4 rows will have 30 × 4 = 120 Tomatoes
Each row has 25 Cabbages
6 rows have 25 × 6 = 150 Cabbages
Each row has 15 Water Lemons
3 rows have 15 × 3 = 45 Water Lemons
In total there 120 + 150 + 45 = 315 plants.
Therefore in Juma’s mother garden there are 315 plants.
Example 14
A
school shop collects sh 90 000 from customers each day. If sh 380 000
from the collection of 6 days was used to buy books. How much money was
left?
school shop collects sh 90 000 from customers each day. If sh 380 000
from the collection of 6 days was used to buy books. How much money was
left?
Each day the collection is sh 90 000
6 days collection is sh 90 000 × 6 = sh 540 000
The money left will be = Total collection – Money used
= sh 540 000 – sh 380 000 = sh 160 000
Therefore the money left was sh 160 000
Exercise 1
1. For each of the following numbers write the place value of a digit in a bracket.
- 899 482 (4)
- 1 940 (0)
- 9 123 476
2. Write the numerals for each of the following problems.
- Ten thousand and fifty one.
- Nine hundred thirty millio
Factors And Multiples Of Numbers
Factors of a Number
Find factors of a number
Consider
two numbers 5 and 6, when we multiply these numbers i.e. 5 6 the answer
is 30. The numbers 5 and 6 are called factors or divisors of 30 and
number 30 is called a multiple of 5 and 6. Therefore factors are the
divisors of a number.
two numbers 5 and 6, when we multiply these numbers i.e. 5 6 the answer
is 30. The numbers 5 and 6 are called factors or divisors of 30 and
number 30 is called a multiple of 5 and 6. Therefore factors are the
divisors of a number.
Example 15
Find all factors of 12
Note that, when listing the factors we don’t repeat any of it.
Multiples of a Number
Find multiples of a number
Multiples
of a number are the products of a number. For example multiples of 4
are 4, 8, 12, 16, 20, 24, … This means multiply 4 by 1, 2, 3, 4, 5, 6, …
.
of a number are the products of a number. For example multiples of 4
are 4, 8, 12, 16, 20, 24, … This means multiply 4 by 1, 2, 3, 4, 5, 6, …
.
Example 16
Example
List all multiples of 6 between 30 and 45.
Solution
The multiples of 6 are: 6×1 = 6; 6×2 = 12; 6×3 = 18; 6×4 = 24; 6×5 = 30; 6×6 = 36; 6×7 = 42; 6×8 = 48 and so on.
Therefore, multiples of 6 between 30 and 45 are 36 and 42.
Factors to Find the Greatest Common Factors(GCF) of Numbers
Use factors to find the greatest common factors(GCF) of numbers
Greatest
Common Factor is sometimes called Highest Common Factor. Its short form
is (GCF) or (HCF) respectively. The Greatest Common Factor is the
largest common divisor of two or more numbers given.
Common Factor is sometimes called Highest Common Factor. Its short form
is (GCF) or (HCF) respectively. The Greatest Common Factor is the
largest common divisor of two or more numbers given.
For
example if you are told to find the GCF of 15 and 25. First, list all
factors or divisors of 15 and that of 25. Thus, factors of 15 are 1, 3,
5, 15factors of 25 are 1, 5, 25
example if you are told to find the GCF of 15 and 25. First, list all
factors or divisors of 15 and that of 25. Thus, factors of 15 are 1, 3,
5, 15factors of 25 are 1, 5, 25
The common factors are 1 and 5. Therefore the GCF is 5.
Example 17
Example1
Find the HCF of 72 and 120.
Solution
We have to list factors of our numbers:
Factors of 72 are 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Factors of 120 are 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120
The common factors are 1, 2, 3, 4, 6, 8, 12, 24.
Therefore the HCF of 72 and 120 is 24.
Another method which can be used to find the GCF or HCF is prime factorization method.
Example 18
Example
Find the HCF of 36 and 48.
Solution
We have to find prime factors of 36 and 48 first
thus, 36 = 2×2×3×3.
48 = 2×2×2× 2×3.
After
writing the numbers as a product of their prime factors, take only the
common prime factors (prime factors appeared to all numbers). In our
example the common factors are 2×2×3. Therefore the HCF of 36 and 48 is
12.
writing the numbers as a product of their prime factors, take only the
common prime factors (prime factors appeared to all numbers). In our
example the common factors are 2×2×3. Therefore the HCF of 36 and 48 is
12.
Lowest Common Multiple (LCM)
Lowest
Common Multiple is also called Least Common Multiple and its short form
is LCM.For example: multiples of 5 are 5, 10, 15, 20, 25, 30, 35, 40,
45, 50, 55, …multiples of 3 are 3, 9, 15, 18, 21, 24, 27, 30, 33, ….
Common Multiple is also called Least Common Multiple and its short form
is LCM.For example: multiples of 5 are 5, 10, 15, 20, 25, 30, 35, 40,
45, 50, 55, …multiples of 3 are 3, 9, 15, 18, 21, 24, 27, 30, 33, ….
When
you look carefully at these multiples of 5 and 3 you notes that 15 had
appeared to both. This multiple which appear to both is called a common
multiple. If there are more than one common multiples which appeared the
smaller common multiple is what is called Lowest Common Multiple.
you look carefully at these multiples of 5 and 3 you notes that 15 had
appeared to both. This multiple which appear to both is called a common
multiple. If there are more than one common multiples which appeared the
smaller common multiple is what is called Lowest Common Multiple.
Example 19
Find the common multiples and then show the Lowest Common Multiple of the numbers 4, 6 and 8.
Solution
Multiples of 4 are 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, …
Multiples of 6 are 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, …
Multiples of 8 are 8, 16, 24, 32, 40, 48, 56, 64, 72, …
The common multiples of 4, 6 and 8 are 24, 48, …
Therefore the Lowest Common Multiple of 4, 6, and 8 is 24.
We
can find the Lowest Common Multiple (LCM) of numbers by writing the
numbers as a product of their prime factors. The method is called prime
factorization.
can find the Lowest Common Multiple (LCM) of numbers by writing the
numbers as a product of their prime factors. The method is called prime
factorization.
Example 20
Find the LCM of 24 and 36 by prime factorization method.
Solution
Let us find prime factors of each number by dividing the numbers by their prime factors.
Now
take the prime factors which appear to both numbers i.e. 2×2×3 (we take
without repeating). We are left with 2 which is a multiple of 24 and 3
which is a multiple 36. We have also to multiply these prime factors
left i.e. 2×2×2×3×3. This gives 72. Therefore the LCM of 24 and 36 is
2×2×2×3×3= 72.
take the prime factors which appear to both numbers i.e. 2×2×3 (we take
without repeating). We are left with 2 which is a multiple of 24 and 3
which is a multiple 36. We have also to multiply these prime factors
left i.e. 2×2×2×3×3. This gives 72. Therefore the LCM of 24 and 36 is
2×2×2×3×3= 72.
Integers
Identify integers
Consider a number line below
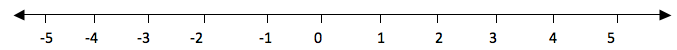
The
numbers from 0 to the right are called positive numbers and the numbers
from 0 to the left with minus (-) sign are called negative numbers.
Therefore all numbers with positive (+) or negative (-) sign are called
integers and they are denoted by Ζ. Numbers with positive sign are
written without showing the positive sign. For example +1, +2, +3, …
they are written simply as 1, 2, 3, … . But negative numbers must carry
negative sign (-). Therefore integers are all positive and negative
numbers including zero (0). Zero is neither positive nor negative
number. It is neutral.
numbers from 0 to the right are called positive numbers and the numbers
from 0 to the left with minus (-) sign are called negative numbers.
Therefore all numbers with positive (+) or negative (-) sign are called
integers and they are denoted by Ζ. Numbers with positive sign are
written without showing the positive sign. For example +1, +2, +3, …
they are written simply as 1, 2, 3, … . But negative numbers must carry
negative sign (-). Therefore integers are all positive and negative
numbers including zero (0). Zero is neither positive nor negative
number. It is neutral.
The
numbers from zero to the right increases their values as the increase.
While the numbers from zero to the left decrease their values as they
increase. Consider a number line below.
numbers from zero to the right increases their values as the increase.
While the numbers from zero to the left decrease their values as they
increase. Consider a number line below.
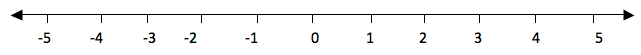
If
you take the numbers 2 and 3, 3 is to the right of 2, so 3 is greater
than 2. We use the symbol ‘>’ to show that the number is greater than
i. e. 3 >2(three is greater than two). And since 2 is to the left of
3, we say that 2 is smaller than 3 i.e. 2<3. The symbol ‘<’ is
use to show that the number is less than.
you take the numbers 2 and 3, 3 is to the right of 2, so 3 is greater
than 2. We use the symbol ‘>’ to show that the number is greater than
i. e. 3 >2(three is greater than two). And since 2 is to the left of
3, we say that 2 is smaller than 3 i.e. 2<3. The symbol ‘<’ is
use to show that the number is less than.
Consider
numbers to the left of 0. For example if you take -5 and -3. -5 is to
the left of -3, therefore -5 is smaller than -3. -3 is to the right of
-5, therefore -3 is greater than -5.
numbers to the left of 0. For example if you take -5 and -3. -5 is to
the left of -3, therefore -5 is smaller than -3. -3 is to the right of
-5, therefore -3 is greater than -5.
Generally, the number which is to the right of the other number is greater than the number which is to the left of it.
If
two numbers are not equal to each to each other, we use the symbol ‘≠’
to show that the two numbers are not equal. The not equal to ‘≠’ is the
opposite of is equal to ‘=’.
two numbers are not equal to each to each other, we use the symbol ‘≠’
to show that the two numbers are not equal. The not equal to ‘≠’ is the
opposite of is equal to ‘=’.
Example 21
Represent the following integers Ζ on a number line
- 0 is greater than Ζ and Ζ is greater than -4
- -2 is less than Ζ and Ζ is less than or equal to 1.
Solution
a.
0 is greater than Ζ means the integers to the left of zero and Ζ is
greater than -4 means integers to the left of -4. These numbers are -1,
-2 and -3. Consider number line below
0 is greater than Ζ means the integers to the left of zero and Ζ is
greater than -4 means integers to the left of -4. These numbers are -1,
-2 and -3. Consider number line below
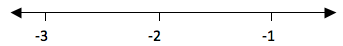
b.
-2 is less than Ζ means integers to the right of -2 and Ζ is less than
or equal to 1 means integers to the left of 1 including 1. These
integers are -1, 0 and 1. Consider the number line below
-2 is less than Ζ means integers to the right of -2 and Ζ is less than
or equal to 1 means integers to the left of 1 including 1. These
integers are -1, 0 and 1. Consider the number line below
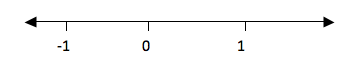
Example 22
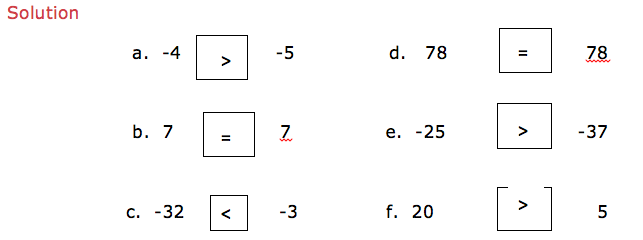
Put the signs ‘is greater than’ (>), ‘is less than’ (<), ‘is equal to’ (=) to make a true statement.
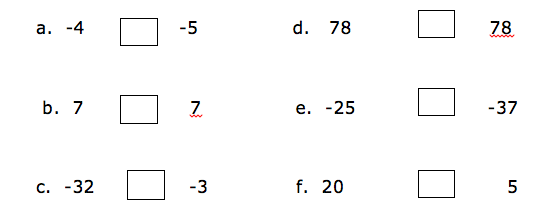
Addition of Integers
Add integers
Example 23
2 + 3
Show a picture of 2 and 3 on a number line.
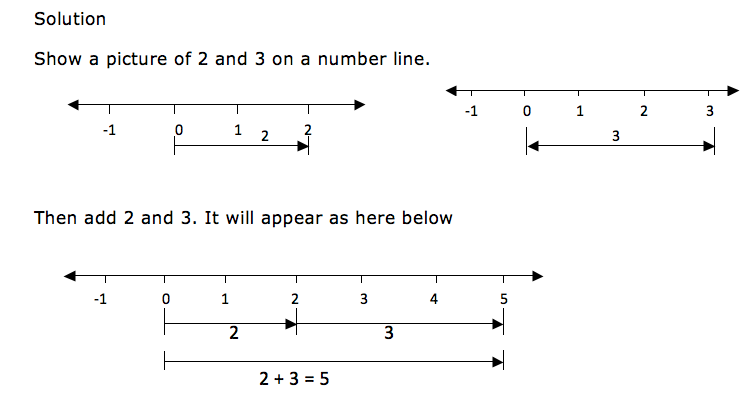
When
drawing integers on a number line, the arrows for the positive numbers
goes to the right while the arrows for the negative numbers goes to the
left. Consider an illustration bellow.
drawing integers on a number line, the arrows for the positive numbers
goes to the right while the arrows for the negative numbers goes to the
left. Consider an illustration bellow.
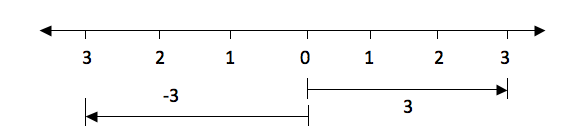
The
distance from 0 to 3 is the same as the distance from 0 to -3, only the
directions of their arrows differ. The arrow for positive 3 goes to the
right while the arrow for the negative 3 goes to the left.
distance from 0 to 3 is the same as the distance from 0 to -3, only the
directions of their arrows differ. The arrow for positive 3 goes to the
right while the arrow for the negative 3 goes to the left.
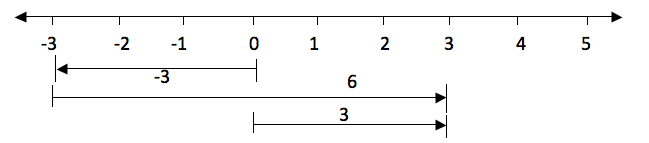
Example 24
-3 + 6
Solution
Subtraction of Integers
Subtract integers
Since
subtraction is the opposite of addition, if for example you are given
5-4 is the same as 5 + (-4). So if we have to subtract 4 from 5 we can
use a number line in the same way as we did in addition. Therefore 5-4
on a number line will be:
subtraction is the opposite of addition, if for example you are given
5-4 is the same as 5 + (-4). So if we have to subtract 4 from 5 we can
use a number line in the same way as we did in addition. Therefore 5-4
on a number line will be:
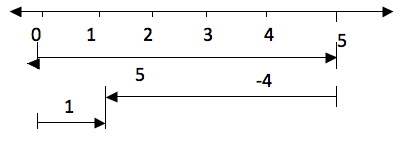
Take five steps from 0 to the right and then four steps to the left from 5. The result is 1.
Multiplication of Integers
Multiply integers
Example 25
2×6 is the same as add 2 six times i.e. 2×6 = 2 + 2 + 2 + 2 + 2 +2 = 12. On a number line will be:
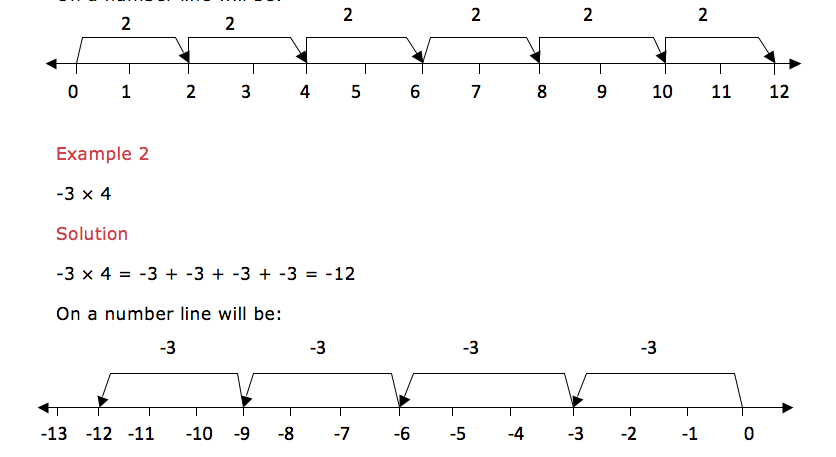
Multiplication
of a negative integer by a negative integer cannot be shown on a number
line but the product of these two negative integers is a positive
integer.
of a negative integer by a negative integer cannot be shown on a number
line but the product of these two negative integers is a positive
integer.
From
the above examples we note that multiplication of two positive integers
is a positive integer. And multiplication of a positive integer by a
negative integer is a negative integer. In summary:
the above examples we note that multiplication of two positive integers
is a positive integer. And multiplication of a positive integer by a
negative integer is a negative integer. In summary:
- (+)×,(+) = (+)
- (-)×,(-) = (+)
- (+)×,(-) = (-)
- (-)×,(+) = (-)
Division of Integers
Divide integers
Example 26
6÷3 is the same as saying that, which number when you multiply it by 3 you will get 6, that number is 2, so, 6÷3 = 2.
Therefore
division is the opposite of multiplication. From our example 2×3 = 6
and 6÷3 = 2. Thus multiplication and division are opposite to each
other.
division is the opposite of multiplication. From our example 2×3 = 6
and 6÷3 = 2. Thus multiplication and division are opposite to each
other.
Dividing
two integers which are both positive the quotient (answer) is a
positive integer. If they are both negative also the quotient is
positive. If one of the integer is positive and the other is negative
then the quotient is negative. In summary:
two integers which are both positive the quotient (answer) is a
positive integer. If they are both negative also the quotient is
positive. If one of the integer is positive and the other is negative
then the quotient is negative. In summary:
- (+)÷(+) = (+)
- (-)÷(-) = (+)
- (+)÷(-) = (-)
- (-)÷(+) = (-)
Mixed Operations on Integers
Perform mixed operations on integers
You
may be given more than one operation on the same problem. Do
multiplication and division first and then the rest of the signs. If
there are brackets, we first open the brackets and then we do division
followed by multiplication, addition and lastly subtraction. In short we
call it BODMAS. The same as the one we did on operations on whole
numbers.
may be given more than one operation on the same problem. Do
multiplication and division first and then the rest of the signs. If
there are brackets, we first open the brackets and then we do division
followed by multiplication, addition and lastly subtraction. In short we
call it BODMAS. The same as the one we did on operations on whole
numbers.
Example 27
9÷3 + 3×2 -1 =
Solution
9÷3 + 3×2 -1
=3 + 6 -1 (first divide and multiply)
=8 (add and then subtract)
Example 28
(12÷4 -2) + 4 – 7=
Solution
(12÷4 -2) + 4 – 7
=1 + 4 – 7 (do operations inside the brackets and divide first)
=5 – 7 (add)
=2
Wonderful, what a web site it is! This blog gives helpful facts to us, keep it up.
Magnificent goods from you, man. I have understand your stuff previous
to and you are just too excellent. I actually like what you’ve acquired here,
certainly like what you’re saying and the way in which you say
it. You make it enjoyable and you still take care of to keep it
smart. I can’t wait to read far more from you. This is really a
tremendous site.
Hey there! I’m at work browsing your blog from my new apple
iphone! Just wanted to say I love reading through your blog and look forward to
all your posts! Keep up the great work!
I visited several websites except the audio quality for audio songs existing at
this website is in fact marvelous. 0mniartist asmr
It’s an amazing post designed for all the internet
users; they will take benefit from it I am sure. asmr 0mniartist
Hello there! I just want to offer you a big thumbs up for your great info
you’ve got here on this post. I will be coming back to your web site for
more soon. 0mniartist asmr
Woah! I’m really digging the template/theme of this blog.
It’s simple, yet effective. A lot of times it’s tough to get that “perfect balance” between usability and appearance.
I must say that you’ve done a very good job with
this. Additionally, the blog loads very quick for me on Firefox.
Outstanding Blog! asmr 0mniartist
You actually make it seem so easy together with your presentation however I find this topic to be really something which
I think I’d never understand. It seems too complicated and extremely wide
for me. I am looking ahead in your next submit, I’ll attempt to
get the hold of it! asmr 0mniartist
Well explained …hongera sana